Where “simulation” came from
When did computer scientists start to talk about “simulation” between programs? As of a couple of months ago, the earliest paper I had seen on this topic was Robin Milner’s widely cited IJCAI 1971 paper, “An algebraic definition of simulation between programs”. (That’s the official publisher’s version, but this tech report version seems to have more readable typesetting.)1
Recently, though, I came across this historical overview of bisimulation by Davide Sangiorgi, published in TOPLAS 2009. Sangiorgi’s paper is mainly about bisimulation, but he discusses simulation as a necessary stepping stone to bisimulation. Sangiorgi, who was Milner’s Ph.D. student, had this to say about Milner’s early work on simulation:
Decisive progress towards bisimulation is made by Milner in the 1970’s. Milner transplants the idea of weak homomorphism into the study of the behavior of programs in a series of papers in the early 1970’s ([Milner 1971a, 1971b, 1970], with Milner [1971a] being a synthesis of the previous two). He studies programs that are sequential, imperative, and that may not terminate. He works on the comparisons among such programs. The aim is to develop techniques for proving the correctness of programs, and for abstracting from irrelevant details so that it is clear when two programs are realizations of the same algorithm. In short, the objective is to understand when and why two programs can be considered “intensionally” equivalent.
To this end, Milner proposes (appropriately adapting it to his setting) the algebraic notion of weak homomorphism that we have described in Section 4.1. He renames weak homomorphism as simulation, a term that better conveys the idea of the application in mind. Although the definition of simulation is still algebraic, Milner now clearly spells out its operational meaning. But perhaps the most important contribution in his papers is the proof technique associated to simulation that he strongly advocates. This technique amounts to exhibiting the set of pairs of related states, and then checking the simulation clauses on each pair. The strength of the technique is precisely the locality of the checks that have to be made, in the sense given to locality in Section 2.1. The technique is proposed to prove not only results of simulation, but also results of input/output correctness for programs, as a simulation between programs implies appropriate relationships on their inputs and outputs.
The Milner [1971a] paper that Sangiorgi refers to is the aforementioned IJCAI ‘71 paper that I had been aware of, but Sangiorgi also cites two slightly older papers, one from 1970 and one from 1971. Both of these are listed in Sangiorgi’s bibliography as being unpublished memos from Milner’s time at Swansea University:
MILNER , R. 1970. A formal notion of simulation between programs. Memo 14, Computers and Logic Resarch Group, University College of Swansea, U.K.
MILNER , R. 1971b. Program simulation: An extended formal notion. Memo 17, Computers and Logic Resarch Group, University College of Swansea, U.K.
I couldn’t find digital versions of either of these old memos online. Milner does also cite them both in his IJCAI ‘71 paper, and he says that the IJCAI paper “is a synthesis of the two, and may be read independently”, so I wasn’t particularly worried about missing any useful science by looking only at the IJCAI ‘71 paper rather than the older two. But we’re not in this just for the usefulness, are we?
I asked around on Mastodon to see who might have access to the two memos, and Jeremy Gibbons came through. The two papers were physically located in the Programming Research Group Archive at the University of Oxford’s Computer Science Library:
The Computer Science Library holds the archive of the Programming Research Group (PRG). It is contained in 240 box-files which hold papers and technical reports produced by PRG members and allied computer scientists between the early 1960s and 1980.
Jeremy kindly contacted the library on my behalf, and heroic librarian Aza Ballard-Whyte located the two papers somewhere in those “240 box-files” and personally scanned and emailed them to me on the other side of the planet. To my amazement, they are handwritten, and they are absolutely gorgeous.
They don’t seem to be on the public internet anywhere. I asked Jeremy if it would be okay to share them, and he said he didn’t think it would be a problem. So without further ado, here they are:
The first paper in particular is a delight. Aside from being in Milner’s lovely handwriting, it also has a few of his own handwritten corrections and comments on it, in red and green ink.
I’ve transcribed the first four paragraphs of the first paper below. I hope you will agree with me that what Milner had to say about what programmers do when writing code, and about how programmers think about their programs, is damn near as true in 2025 as it was in 1970.
Programmers often choose an unnatural representation for their data objects, even when a more natural choice exists in the language they are using. Their reason may be that they do not wish to incur the space/time overheads of the more natural choice of data types, particularly when they only use frequently a subset of the operations available over those types – and when that subset is efficiently carried out in terms of a less obvious choice of data representation.
An example of this is in the storage of clauses in a resolution-based theorem-prover. Clauses are naturally sets of formulae, and a formula is naturally a tree or nested list. But because (i) clauses once formed are not normally alterned or extended, and (ii) the frequent operations on clauses – e.g. unification, substitution – are efficiently done on a string or vector representation, one would not except for pedagogic reasons use for clauses the data types set, list even in a languages which had them.
Whatever the reason for choosing an unnatural representation, programmers continue to think in terms of the natural data objects too; it follows that they are aware of the mapping – or whatever it is – that exists between them, however implicitly. Part of the purpose of this paper is to formulate whatever it is explicitly: we show how the real program simulates (in a precise sense) the ideal program that never got written.
Motivation comes from the fact that proving that an ‘unnatural’ program works – a task certainly too hard for complete mechanisation at present except for the most trivial cases – or even expressing what it is supposed to do, appears to involve making the simulation at least partly explicit.
As an example of a program that uses “unnatural” data structures, Milner draws on one of his own even older Swansea memos from 1969 (which I haven’t looked at), appropriately called “The difficulty of verifying a program with unnatural data representation”. The program takes two arrays of characters \(\sigma\) and \(\tau\) and one character argument \(c\), and is supposed to produce a new character array consisting of \(\sigma\) but with all occurrences of \(c\) replaced by \(\tau\). (For instance, if the arguments were "foo", "bar", and 'o', we would get "fbarbar".)
Milner observes that if one writes this program without the help of ‘natural’ data structures, determining that the program is correct involves a fiddly correctness criterion defined in terms of a metafunction he calls “seq”. This example, he says, illustrates how “program verification is most naturally done in terms of the natural data objects”:
If the programmer has in mind, while writing this program, an ‘ideal’ program with a similar flowchart and with string variables, then the values assumed by the latter will roughly correspond to the values of the ‘seq(…)` subexpressions in the assertions. In fact one may hope for a kind of homomorphism from the statespace of the real program to that of the ideal program, since the latter’s variables take values which are functions of those in the former.
What Milner is suggesting here is that the real program, with its “unnatural” data representation, is in some kind of implicit correspondence with some ideal program in the programmer’s head, which has a “natural” data representation – in particular, lists, which, if their elements are characters, are also known as strings. (When it comes to data types, strings might not seem like they’re at a particularly high level of abstraction. But, remember, this was 1970! The C programming language, for example, did not exist yet.)
Milner then goes on to formalize what such correspondences between programs – which he, and generations of computer scientists since, have called simulations – look like when they are made explicit. This is the meat of the paper, and I won’t go into detail about it here. Instead, I want to focus on this absolutely gorgeous hand-drawn figure. Such diagrams are ubiquitous now in program verification textbooks, but this might have been one of the first times that someone drew one!
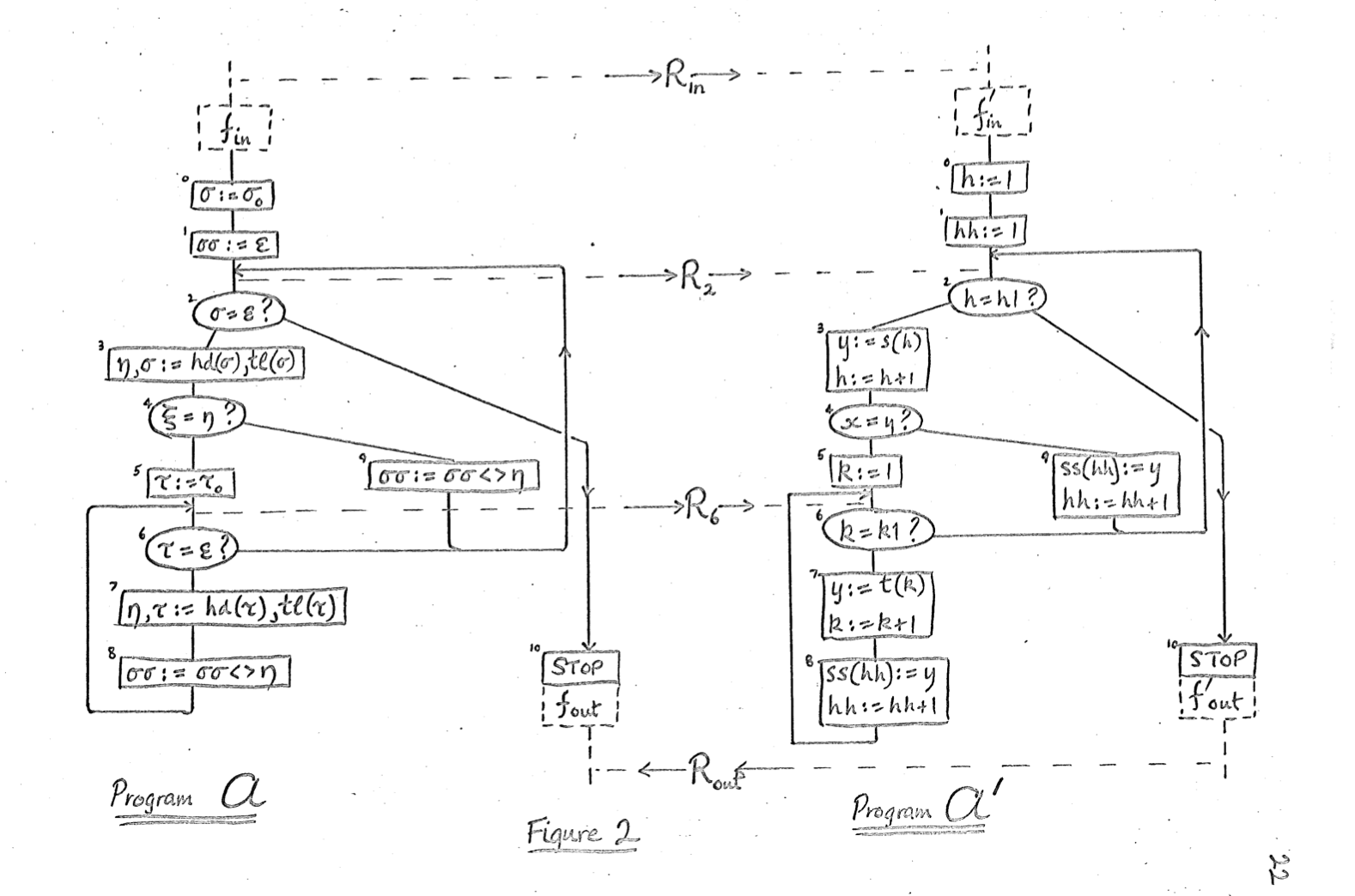
Here, the “real” program \(A'\) (on the right) simulates the “ideal” program \(A\) (on the left) – or, if you like, the “ideal” program \(A\) is simulated by the “real” program \(A'\)). The key thing to notice is how the two programs represent data objects differently. For instance, in the “ideal” program on the left, we see the tell-tale presence of “hd” and “tl”, which are list operations that respectively return the first element of a list and all but the first element of a list (or the first character of a string and all but the first character of a string, if you prefer). The “real” program on the right, \(A'\), does not use those list operations, and is an example of a program in which “the natural data objects were not directly represented”, in Milner’s words. But, once we know that \(A'\) simulates \(A\), then if \(A\) is correct, we know that \(A'\) is correct. Milner concludes section 4 of the paper: “total correctness of \(A\) implies the same for \(A'\)”. Although the example in this 1970 paper is just a toy, it illustrates a powerful idea that lies at the heart of industrial-strength verification efforts based on refinement proofs, like the seL4 OS kernel.
I sent Aza a thank-you postcard with a Santa Cruz beach vista on it.
-
He published this groundbreaking paper while affiliated with Stanford University, and it amuses to me to see that Stanford affiliation on there, because Robin Milner certainly seems to me to have been a quintessentially British person. I wonder what he thought of California during his short time here. ↩

Comments