How to read from an LVar: an illustrated guide
I’ve written a few posts about my work on LVars, which are data structures that support deterministic multithreaded computation. Fundamentally, there are two things to do with an LVar: write to it, and read from it.
When I talk about how LVars work, I usually focus on writes, but they’re only half the story. In this post, we’ll look at how LVar reads work.
LVar basics
An LVar is a memory location that can be shared between multiple threads. Unlike an ordinary shared memory cell whose contents might change arbitrarily, the contents of an LVar can only grow bigger over time, for some definition of “bigger” that the user of the LVar gets to specify.
This increase-only invariant holds because the only way to write to an LVar is by means of a put operation that is defined in terms of that user-specified notion of “bigger”.
For instance, let’s suppose that two parallel threads are writing to a natural-number-valued LVar called num, with one thread writing 2 and the other writing 3. Here, let par launches parallel subcomputations that run in arbitrary order, and in is a synchronization barrier.
let par _ = put num 3
_ = put num 2
in get num (* deterministic -- always 3 *)
When we put a value into an LVar, it ends up as the bigger of the old and new values. Therefore, if we try to put a value that’s smaller than, or equal to, what’s already there, our put has no effect. So, if num’s notion of “bigger” is the standard “greater than or equal to” that you’d expect it to be for 2 and 3, then the semantics of LVar writes will ensure that the contents of the LVar will end up as 3, regardless of the order in which those two writes take place.
The idea that 3 is bigger than 2 is part the notion of “bigger” that we specify (in some other piece of code, perhaps) when we use an LVar. So, if we wanted to, we could instead define an order in which 3 is less than 2, in which case this program would deterministically evaluate to 2. Or we could define an ordering in which 2 and 3 conflict with each other, in which case it would deterministically raise a run-time error. The point is that the program will behave deterministically regardless of the notion of “bigger” that we choose to plug in.
Crossing the threshold
So, we have a semantics that only allows monotonically increasing writes to LVars. By itself, though, that isn’t enough to ensure that programs are deterministic. For instance, in our example, suppose we allow the get num call to be interleaved with the two puts.
let par _ = put num 3
_ = put num 2
x = get num
in x (* nondeterministic -- could be 2 or 3 *)
This program is nondeterministic, despite writes always being monotonically increasing. In particular, get might read either 2 or 3, depending on the whim of the scheduler and how it decides to order the put and get operations.
So, to maintain determinism, we have to put an extra restriction on the get operation, as follows: when we read from an LVar using get, we aren’t allowed to read the LVar’s exact value, but, rather, one of a set of lower bounds on its value. We’ll have to specify this set of lower bounds as an extra argument to get. Moreover, the get operation must block until the LVar reaches a value that is at or above one of those lower bounds.
For our num example, the set of lower bounds we’ll pass to get is just the singleton set { 3 }. We call this set a threshold set, because the values in it (in this case, just 3) form a “threshold” beyond which the call to get is allowed to unblock and return a result. And we refer to the kind of read that the get operation does as a threshold read, because the value it returns is the threshold we’ve crossed.
let par _ = put num 3
_ = put num 2
x = get num { 3 } (* blocks until we're at or above 3 *)
in x (* deterministic -- always 3 *)
Since num’s value can only increase with time, we know that once it is at least 3, it will remain at or above 3 forever. So, as long as we only access them through the put/get interface, LVars are thread-safe: we can safely share them between threads without introducing unintentional nondeterminism. That is, puts and gets can happen in any order, without changing the value that a program evaluates to.
But what good are threshold reads?
A call like get num { 3 } doesn’t seem all that useful. It will let us find out when num’s value is at least 3, but we have no way of knowing whether num’s actual value is 3 or 4 or eleventy billion. Still, even this extremely restricted interface serves some useful purposes.

For instance, let’s say that Horace, Franz, and Kat are three grad students who spend a lot of late nights working in the lab. On these late nights, it’s often the case that one of them is interested in having pizza delivered – but only if the others are both planning to help eat it, since it’s preferable not to let food sit around the lab uneaten.1 So, how should they decide when to call for a pizza?
Quorum voting
To solve this problem, they can implement a simple quorum voting system in which several threads share an LVar, say, pizza_votes. First, we have a vote-collecting thread. It waits for confirmation that all three of them have voted, then calls the pizza place.
(* Vote-collecting thread *)
let _ = get pizza_votes { { Horace, Franz, Kat } }
in call_for_pizza(large, extra_cheese)
We also have several voting threads that don’t run immediately, but are launched by, say, clicking a button on a web form that sends a unique identifier for the person using the form – in this case, the person’s name.
(* Voting thread for Horace *)
put pizza_votes { Horace }
(* Voting thread for Franz *)
put pizza_votes { Franz }
(* Voting thread for Kat *)
put pizza_votes { Kat }
The states that pizza_votes can take on form a lattice, ordered by set inclusion. The lattice captures the user-specified notion of “bigger” for this LVar: higher in the lattice is bigger.
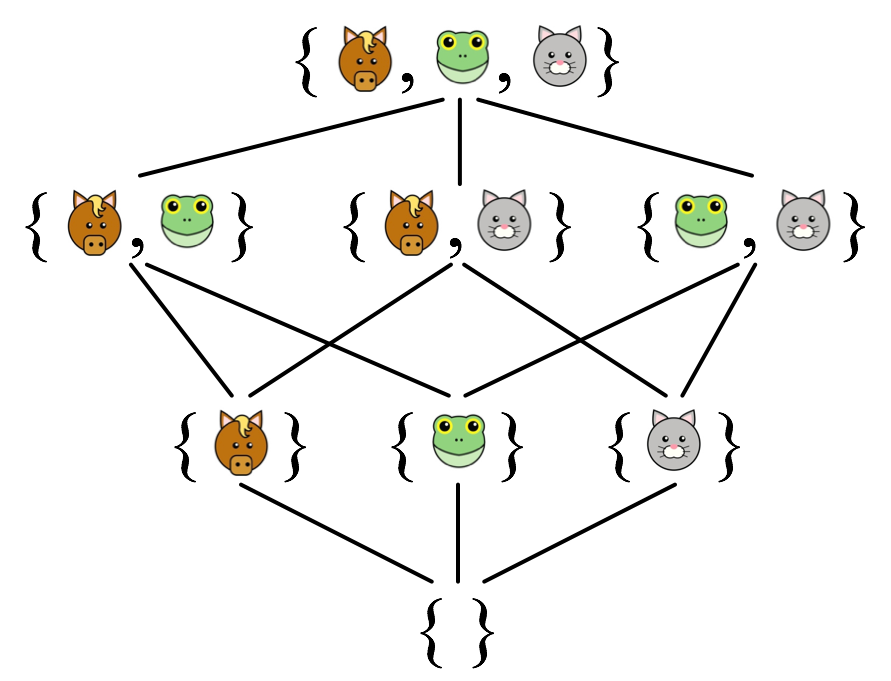
From this diagram, it’s easy to see that the order in which Horace, Franz, and Kat vote, if they vote at all, doesn’t matter. For instance, if Horace votes first, followed by Franz, we’ll take the least upper bound of { Horace } and { Franz }, which is the smallest element that is at or above both { Horace } and { Franz }. That element, of course, is { Horace, Franz }.
This raises an interesting point about put. In the case of our natural-number-valued LVar, num, we never encounter a situation where two values being written don’t have an order, because, given any two distinct natural numbers x and y that we might be writing to num, it’s always going to be the case that either x < y, or y < x.
But this property isn’t true of the values that pizza_votes can take on. In general, we have to be able to deal with situations where a put to an LVar occurs and neither the new nor the old value is bigger. In other words, the set of states that an LVar can take on is a partially ordered set, not necessarily a totally ordered one.
So, given two states where neither is above the other in the lattice – such as { Horace } and { Franz } – we need to be able to deterministically merge those two states into a new state that’s bigger than both. This “deterministic merge” is exactly the least-upper-bound operation.
Because we might need to be able to merge any two states, we require that in the set of states that an LVar can take on, every two states have a least upper bound.2 And, since least upper bounds are unique, we know that such a merge will be deterministic.
Returning to our example, if the current state of pizza_votes is { Horace, Franz } and Kat votes next, the state of pizza_votes becomes the least upper bound of { Horace, Franz } and { Kat }, which is { Horace, Franz, Kat }. If the votes had happened in the opposite order, we would have gone from { Kat } to { Franz, Kat } to { Horace, Franz, Kat }. Since we end up in the same state either way, the intermediate states don’t matter. In fact, they can’t matter, since they aren’t observable by get.
What if, say, Franz decides not to vote? Then quorum will never be reached, no matter what Horace and Kat do. On the other hand, if Franz clicks the “vote” button a thousand times, whether out of impatience or just because he was accidentally leaning on the Enter key, then no harm is done, because the least upper bound of { Franz } and any set S already containing Franz is merely S – so it’s impossible to vote twice.
Determinism and observable results
We define a program to be deterministic if, given the same inputs, it will always produce the same observable result. Here, inputs are votes, and we define the observable result of a program to be the value to which it evaluates. We’ve therefore cheated a bit with our call to call_for_pizza, since it triggers a side effect, and our determinism guarantee doesn’t say anything about side effects.
To assure ourselves that this cheat is innocuous, we can suppose that call_for_pizza doesn’t perform a side effect, and instead merely evaluates to a string, say, "Hey, call the pizza place". We can guarantee that for any given set of votes, regardless of the order in which those votes arrive, our program will deterministically do one of two things: return that string, or never return at all because it’ll still be waiting to receive a vote.
More interesting threshold sets
Update (December 24, 2013): There’s a subtle bug in the example in this section! Read “The LVar that wasn’t” for more details.
So far, all the threshold sets we’ve seen have been singleton threshold sets. That means that, for all the calls to get that we’ve seen so far, there’s only one value that get might return: the sole member of the threshold set. But to ensure determinism, it is not necessary in general for threshold sets to be singleton sets! Let’s look at an example where the threshold set has two elements.
Suppose that, sooner or later, it becomes clear to Horace, Franz, and Kat that it’s not necessary to wait to order a pizza until all three of them have committed to helping eat it. As it turns out, any one of them is more than capable of eating a pizza on their own. As a matter of fact, the only situation in which they should absolutely not get a pizza is one in which all three of them have explicitly vetoed the idea. (Really, they should have been doing it this way all along.)
So, they decide to redesign the voting system to work as follows:
- Start with everyone’s vote unknown.
- If anyone votes for pizza, then send for a pizza and end the program.
- If everyone votes against pizza, then stop polling and end the program.
- Otherwise, voting remains open until one of the above two conditions are met.
Under the new system, each voter, if they choose to vote at all, now has the option of voting for or against pizza. But those two cases are not quite symmetric. For instance, the code that runs when Horace votes against pizza would be something like
put pizza_votes { horace_no }
because we have to record who the vote came from. But in case of a vote in favor, we don’t have to worry about who it’s from:
put pizza_votes yes
Under this scenario, the states that pizza_votes can take on form a differently-shaped lattice.
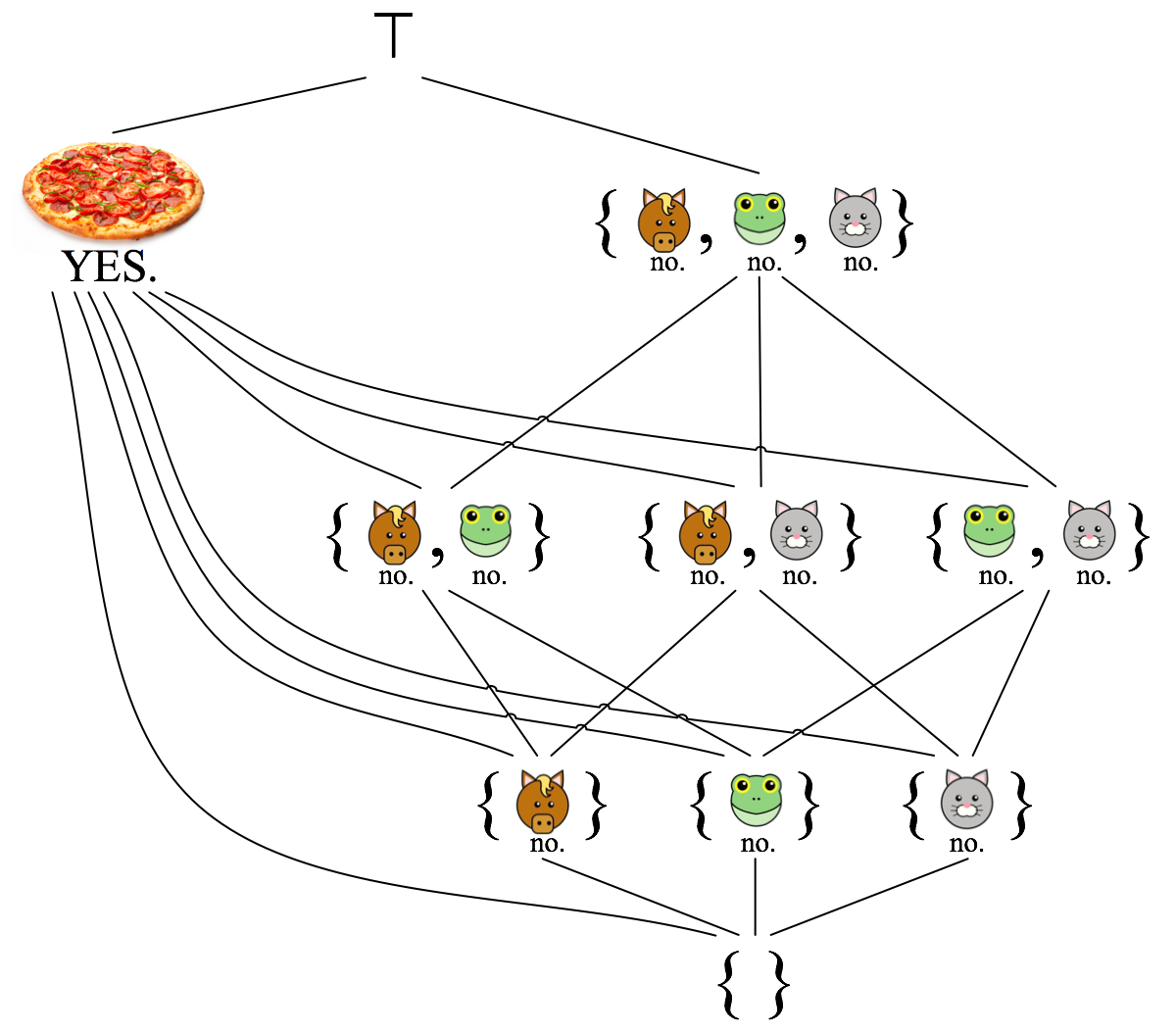
If anyone votes for pizza, we jump right to the yes state, and we needn’t bother to collect any more votes. If it so happens that the other two votes come in before we stop collecting votes, though, then it’s no problem, because the least upper bound of yes and any two other votes is just yes! This implements the “If anyone votes for pizza, then send for a pizza and end the program” part of the specification.
Our vote-collecting thread looks a little different as well. There are now two states that could trigger the program to end: either someone has voted yes, or everyone has voted no. Correspondingly, the threshold set we pass to pizza_votes has two elements.
(* Vote-collecting thread *)
let x = get pizza_votes { yes, { horace_no, franz_no, kat_no } }
in
if (x == yes)
call_for_pizza(large, extra_cheese)
else
() (* don't do anything; return unit *)
For a given set of votes, only one of yes or { horace_no, franz_no, kat_no } can ever be reached, so this program will behave deterministically regardless of the order in which the votes are received.
The top element and incompatibility of threshold sets
In addition to the yes element, we’ve also added a top element ⊤ (pronounced “top”) to the pizza_votes lattice.3 During normal execution, we would never reach the top element. We can think of it as an error state: a sign that something has gone wrong. The put operation deals specially with ⊤, as we’ll see in a moment.
Whenever we have a threshold set of more than one element, as we do here, it must be the case that, for any two elements of the threshold set, their least upper bound is the top element. That is, for every pair of elements in the threshold set, those elements must be incompatible with each other: there must be no way for them to both be true at the same time.
This models the idea that it should never be the case that more than one element of a threshold set can be unblocked at once. When a get operation on an LVar unblocks, there will always be a unique element of the threshold set that the actual state of the LVar is at or above, and the get operation will return that unique element.
This uniqueness is crucial for determinism. To see why, consider what would happen if we tried to do the following get on pizza_votes:
get pizza_votes { { horace_no }, { kat_no } }
Here, we’re trying to find out if either Horace or Kat, or both, have vetoed pizza. Suppose that both Horace and Kat do, in fact, vote against pizza. That would mean that the following puts run at some point, in some order:
put pizza_votes { horace_no }
put pizza_votes { kat_no }
What happens when these two puts are interleaved with get pizza_votes { { horace_no }, { kat_no } } in some arbitrary order, depending on what the scheduler decides to do? The get might unblock and return horace_no on some runs or kat_no on others, depending on which put has already completed. And what do we do if both puts have completed at the time we run get? How will it know which element to return?
The problem here is that { { horace_no }, { kat_no } } contains two elements whose least upper bound is not ⊤. (Specifically, their least upper bound is { horace_no, kat_no }.) Intuitively, we can see that it’s a bad threshold set because there is a way for its two elements to coexist.
On the other hand, the threshold set of { yes, { horace_no, franz_no, kat_no } } in our vote-collecting code is fine, because there is no possibility of yes and { horace_no, franz_no, kat_no } being true at the same time, no matter what order votes arrive in.
Error handling
If all communication between threads happens through LVars, is it possible to write a nondeterministic program?
To be sure, there’s nothing stopping anyone from writing a program like the following.
let par _ = put pizza_votes { horace_no, franz_no, kat_no };
_ = put pizza_votes yes
x = get pizza_votes { yes, { horace_no, franz_no, kat_no } }
in x
Here, we haven’t written any illegal threshold sets, but we have tried to write two incompatible elements to pizza_votes. If the program were allowed to evaluate to the value of x, then it would be nondeterministic, because x might be either yes or { horace_no, franz_no, kat_no } depending on how the reads and writes are scheduled.
But we’ll never get that far, because of the way that the put operation deals with ⊤. Regardless of the order of the two calls to put, as soon as the second put tries to run, the lattice will reach the ⊤ state, in which case put will raise an error. The program will bail out with an error message, rather than continuing on past the in synchronization barrier.
The top element is a big, heavy hammer of determinism. We can think of ⊤ as meaning, “Hey, something just happened that’s so bad, there’s no way I can promise to remain deterministic if I keep running. So I’m going to force myself to remain deterministic by bailing on execution, right now, before it’s too late!”
Conclusion
In this post I’ve tried to explain how LVar reads work. Threshold sets are the trickiest thing about LVars, and I’m always trying to come up with better ways to explain them. Please, let me know in comments if I’ve made any mistakes, or if anything here was particularly difficult to understand. You can also find more examples of LVar reads, including some with infinite threshold sets, in our paper draft.
Thanks for reading!
-
In practice, of course, the pizza would never go uneaten, but just bear with me. ↩
-
Therefore, the set of states that an LVar can take on actually has to be a join-semilattice, which is a partially ordered set in which every two elements have a least upper bound. We usually just use the word “lattice” for brevity, though. ↩
-
Formally, we require that every LVar has a special top element representing an error state, but for some LVars (like the original version of
pizza_votes, ornum), that top element can never be reached, which follows from the fact that it’s impossible to do two unmergeable writes to those LVars. I left the top element out of the firstpizza_votesdiagram, but it wouldn’t do any harm to have it in there, right above the{ Horace, Franz, Kat }state. ↩

Comments