When is causal broadcast not enough for causal memory?
While getting ready to teach my grad distributed systems course this fall, I found myself once again flipping through Cheriton and Skeen’s rather scathing 1993 article “Understanding the limitations of causally and totally ordered communication”.1 One of Cheriton and Skeen’s complaints about causally ordered communication is that it does not enforce the ordering constraints that they care about. They write:
[T]he correct behavior of an application requires ordering constraints over operations on its state, and these constraints are typically stronger than or distinct from the ordering constraints imposed by the happens-before relationship. Such ordering constraints, referred to as “semantic” ordering constraints, run the gamut from weak to strong, and they may or may not require grouping as well. Example constraints include causal memory [1], linearizability [12], and, of course, serializability. Even the weakest of these semantic ordering constraints, causal memory, can not be enforced through the use of causal multicast [1].
While it’s a good point that there are many important application-level ordering relationships that are not captured by the happens-before order, the last sentence above caught my attention because it seemed counterintuitive. Of course we can’t expect the causal order to give us linearizability or serializability. But causal memory is a distributed shared memory abstraction in which “reads respect the order of causally related writes”, and it certainly seems like it ought to be the kind of thing you can implement using good old causal-order-enforcing communication primitives. So, why can’t you? Let’s dig in!
The paper that Cheriton and Skeen cite as “[1]” there is “Implementing and programming causal distributed shared memory”, published in 1991 by Ahamad, Hutto, and John. The more often cited paper for “causal memory” is actually not this 1991 paper, but rather, “Causal memory: definitions, implementation, and programming”, a 1995 follow-up with some of the same authors. (Of course, Cheriton and Skeen didn’t cite the 1995 paper, because it did not exist yet when they wrote theirs.) Unfortunately, the 1991 paper is not open access; here’s a copy. In this 1991 paper, Ahamad et al. explain that while causal memory is indeed “closely related” to causal message ordering (which is a perennial topic around here), broadcasting writes and delivering them in causal order doesn’t quite get us causal memory. They write (emphasis mine):
As we have said, causal memory is closely related to the ISIS causal broadcast and, thereby, to the notion of causally ordered messages. But causal memory is more than a collection of “locations” updated by causal broadcasts. There are significant differences in the two models.
One way to relate the two models is to assume that each processor has a copy of the memory (a cache) and writes are sent as broadcast messages to all processors. When a message arrives at a processor, it updates its memory by storing the value contained in the message into the appropriate location. A read by the processor returns the value in its memory. It may seem that when the message delivery order preserves causality (for example by using the causal broadcast protocol of ISIS) the values returned by read operations will satisfy the requirements of causal memory. This, however, is not true.
They then give an example of an execution of this collection-of-locations-updated-by-causal-broadcast-based approach that would not be allowed by causal memory. For me, a Lamport diagram makes their example execution easier to understand, so here’s one, showing broadcasts for writes and the contents of each process’s cache:
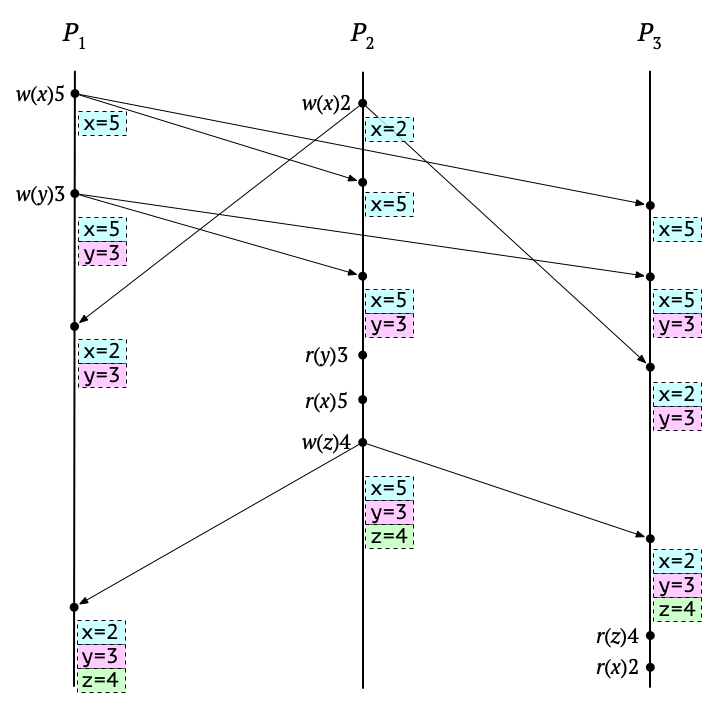
Here, we have three processes, \(P_1\), \(P_2\), and \(P_3\), each of which has carried out a sequence of read and write operations. I’ve borrowed Ahamad et al.’s notation for these: A write operation \(w(x)v\) writes the value \(v\) to location \(x\), and a read operation \(r(x)v\) reads the value \(v\) from location \(x\). The boxes in dashed lines are each process’s local memory, and messages between processes are causal broadcasts, which happen on each write.
The part of this execution that violates causal memory is the read of \(x\) on \(P_3\): \(r(x)2\). From what I can tell, this wouldn’t happen under causal memory, for a subtle reason described earlier in the paper, in section 2:
However, an intervening read operation \(r(x)v'\) serves notice that \(v\) has been overwritten and is sufficient to eliminate \(v\) from \(\alpha(o)\) as well.
Here, “\(\alpha(o)\)” is what Ahamad et al. call the live set for a given read. Under causal memory, every read has to return a value from the live set for that read. Because there could be multiple writes that causally precede a read, in general there might be multiple values in the live set for a read, and under causal memory it’s fine to choose any of them.
In this particular execution, both the write \(w(x)5\) on \(P_1\) and the write \(w(x)2\) on \(P_2\) causally precede the read \(r(x)2\) on \(P_3\). So it seems as though \(5\) and \(2\) should both be in the live set for the read \(r(x)2\). But! There’s an intervening read on \(P_2\) that reads \(5\). That means that \(2\) is eliminated from the live set, and so under causal memory, the read of \(2\) on \(P_3\) would actually be wrong.
A perhaps more intuitive way to explain the issue is as follows: if a process reads a location, then the value it reads has to have come from a causally preceding write on some process. There will be at least one causal path from the write to the read. If there are multiple causal paths to the read from different, concurrent writes, then one of the written values will be read, and under causal memory, it could be either one. But if these multiple causal paths to the read also both pass through some causally preceding “intervening read”, and that intervening read “picks a winner”, then under causal memory, the later read has to pick the same winner!
Here’s the same Lamport diagram, but now with causal paths highlighted to attempt to illustrate the bug:
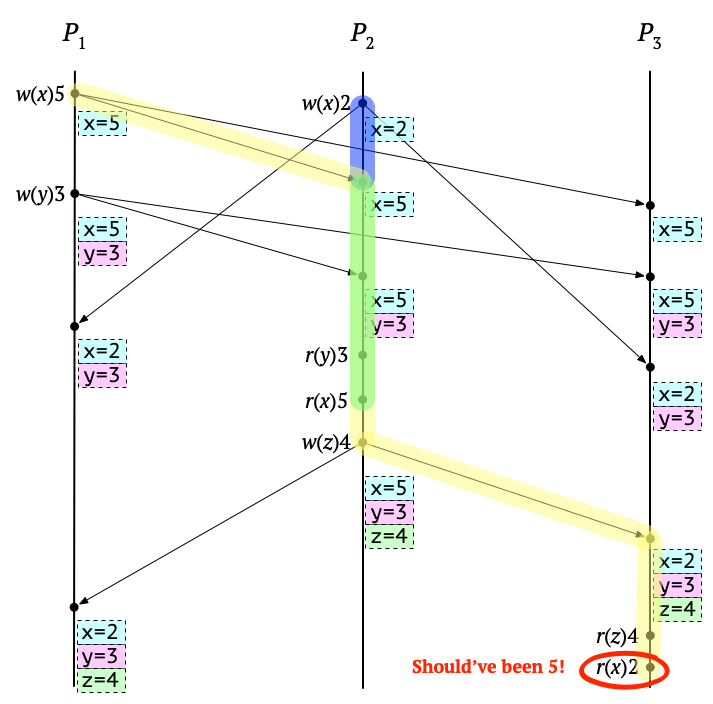
Here, a causal path starting at the write \(w(x)5\) is yellow, and a causal path starting at the write \(w(x)2\) is blue. Both paths are heading for the read of \(x\) on \(P_3\). The paths overlap for a while, as shown in green. But then, during that overlapping part, there’s the read \(r(x)5\) on \(P_2\). Since the “winner” is chosen to be 5 by that read, the causal path starting at \(w(x)2\) has been effectively “cut off”, and now the rest of the causal path can only be yellow. Therefore, under causal memory the read of \(x\) on \(P_3\) should have been 5, and so this is a buggy execution.
So, causal memory admits fewer executions than the set-of-locations-updated-by-causal-broadcasts approach. Although I had read the 1995 causal memory paper, I didn’t realize that this “intervening read operation” thing was a thing – it didn’t sink in for me until looking at this 1991 paper a couple days ago. It’s interesting how a read – not a write, just an innocent little read! – on one process can have an effect on what a different process is allowed to read. My student Jonathan Castello remarked that these so-called reads should really be thought of as just another flavor of write, since they’re effectful.
Perhaps it won’t come as a surprise, then, that in the implementation of causal memory that Ahamad et al. show later in the paper, reads do in fact involve inter-process communication! The implementation enforces the causal memory policy using cache invalidation. Every location has a designated owner process. If you try to read from a location you don’t own, and your cached copy of it is invalid, you have to check in with the owner. It’s not exactly the most “local-first” design, as the kids these days would say.
In exchange, unlike in the set-of-locations-updated-by-causal-broadcasts approach, you can be assured that \(P_3\) will not read \(2\) out of \(x\) if \(P_2\) already read \(5\) out of \(x\). Whether this tradeoff is worthwhile probably depends on what you’re trying to do!
-
Later, Ken Birman wrote an equally scathing response, containing such zingers as, “Transactions have often been viewed as the magic wand that makes all fault-tolerance problems vanish – especially by those who don’t actually build fault-tolerant systems for their living.” ↩

Comments