The LVar that was, after all
Last year, I wrote a post about a so-called LVar data structure that, upon closer inspection, turned out not to be an LVar at all. In that post, I proposed a way to fix the problem, but the fix seemed to be at the expense of another desirable property of the data structure. In this post, I return to that example, but this time, I’ll explain how we can have our cake and eat it, too!
Recap: the lattice that wasn’t
The offending data structure was intended to store the result of a parallel logical “and” operation. It received one write each from two sources, which we could call the “left” and “right” inputs, each of which could be either True or False.
If it received True from both inputs, it would end up in a final state, which we called TrueTrue, indicating that the result was true, and if it received False from at least one input, it would end up in a final state indicating that the result was false, which we just called F.
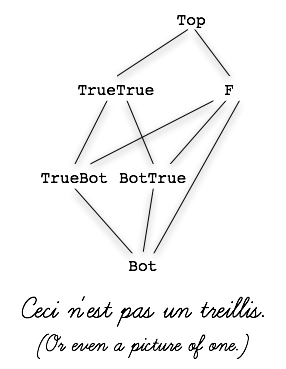
If it received more writes than it expected, and they conflicted – for instance, a True from the left, followed by a True from the right, and after that a False from the left – it would end up in an error state, called Top. And there were also a few intermediate states that it might take on along the way to any of these states, such as a state called TrueBot in which True had been received from the left and nothing else had been received yet, and BotTrue, in which True had been received from the right and nothing else had been received.
We wrote down the set of states that the data structure could take on as a partial order. The trouble was that the partial order wasn’t a join-semilattice, since not all pairs of states had a join; the so-called join operation wasn’t associative and therefore wasn’t actually a join. In particular, the join of BotTrue and F was F, which, joined with TrueBot, was again F. But TrueBot joined with BotTrue was TrueTrue, which, joined with F, was Top. Since the data structure wasn’t a join-semilattice, all bets were off; it couldn’t be an LVar.
In fact, consider that an execution starting with a write of True from the left, then True from the right, and finally False from the left would end in Top, but if the writes happened in a different order – if the execution started with True from the right, followed by False from the left and then True from the left, we’d be in the F state, not Top. Since LVars are supposed to end up in the same state regardless of the order in which writes occur to them, this was Very Bad.
Fortunately, we could define the data structure’s states and the partial order on them differently, and regain associativity and hence LVar status.
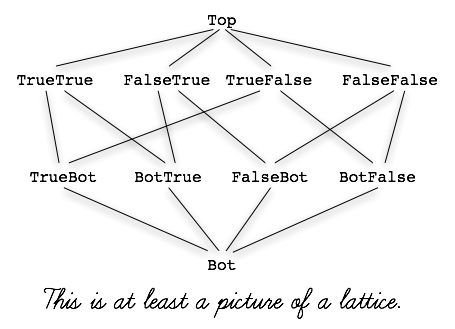
Unfortunately, when we did this, it seemed to be at the price of early answers. The nice thing about the original formulation was that it let us threshold on the states TrueTrue and F, so that as soon as we reached either one, we could “short circuit” and return a result. In particular, in the original formulation, if we ever got a write of False from either the left or the right input, a threshold read could return F as soon as that write of False happened, by using { TrueTrue, F } as its threshold set.
But with the lattice-that’s-really-a-lattice, we couldn’t return anything upon reaching the FalseBot or BotFalse states. Instead, we would have to wait until reaching one of the final states of FalseTrue, TrueFalse, or FalseFalse, even though FalseBot and BotFalse also amount to false.
Fortunately, it turns out there is a way to get short-circuiting behavior from a lattice like this! It requires a slight change to how threshold reads work. Let’s take a look.
Threshold reads and activation sets
First, let’s review what a threshold read does. The goal of a threshold read is to make it so that when we read from a data structure, the result will be a deterministic function of the set of all writes to the data structure that occur in the entire execution. The order in which those writes occur, and the order in which the read is interleaved with the writes, shouldn’t matter. It’s kind of a tall order. How do we accomplish this?
One way to do it is to define a threshold set for the read. A threshold set is a set of what we call activation sets, each consisting of what we call activation states. In the case of our parallel “and” computation, one of those activation sets is the set of states that the data structure might be in when at least one False has been written:
{
FalseBot,BotFalse,FalseTrue,TrueFalse,FalseFalse}
When we reach a point in the lattice that’s at or above any of these states, then we know that the result is false. The other activation set is the singleton set
{
TrueTrue}
When we reach TrueTrue, we know that the result is true. But we have to wait until then, because we don’t know if the result is true unless both the left and right inputs have each contributed True. So a state like TrueBot doesn’t appear in any of our activation sets.
The threshold set is, again, a set of all the activation sets. So the entire threshold set we’d use for reading from our lattice would be:
{ {
FalseBot,BotFalse,FalseTrue,TrueFalse,FalseFalse}, {TrueTrue} }
Using this threshold set, we can do a threshold read. The semantics of a threshold read is as follows: if the data structure’s state reaches (or surpasses) any state or states in a particular activation set, then the threshold read returns that entire activation set, regardless of which of its activation states were reached. If no state in any activation set has yet been reached, the threshold read will block.
In our case, as soon as either input writes False, our threshold read will unblock and return the first activation set. Hence we have the short-circuiting behavior that we want; we don’t have to wait for a second input if the first input is False. If, on the other hand, both inputs write True, the threshold read will unblock and return { TrueTrue }.
In a real implementation, of course, the value returned from the threshold read could be more meaningful to the client – for instance, we could just return False or True instead of returning an activation set. But the translation from { FalseBot, BotFalse, FalseTrue, TrueFalse, FalseFalse } to False could just as easily take place on the client side. In either case, the result returned from the threshold read is the same regardless of which of the activation states caused it to unblock, and it is impossible for the client to tell whether the actual state of the lattice is, say, TrueFalse or FalseFalse or some other state containing False.
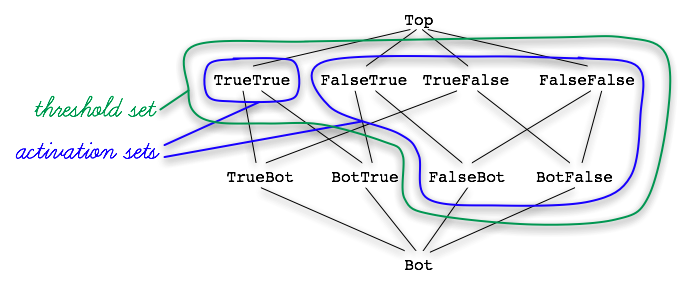
Incompatibility
In order for the behavior of a threshold read to be deterministic, it must be unblocked by a unique activation set in the threshold set. We ensure this by requiring that elements in an activation set must be pairwise incompatible with elements in every other activation set. That is, for all distinct activation sets Q and R in a given threshold set: for all q in Q and for all r in R, the join of q and r is the greatest element of the lattice, in this case, Top. In our running example, we have two distinct activation sets, so if we let Q be { TrueTrue } and let R be { FalseBot, BotFalse, FalseTrue, TrueFalse, FalseFalse }, the join of TrueTrue and r must be Top, where r is any element of R. We can easily verify that this is the case. Furthermore, since the lattice of states that our data structure can take on is finite, we can quickly verify that our join function actually computes a least upper bound, as we’ve seen before.
Why is incompatibility necessary? Consider the following (illegal) “threshold set” that does not meet the incompatibility criterion:
{ {
FalseBot,BotFalse}, {TrueBot,BotTrue} }
A threshold read corresponding to this so-called “threshold set” will unblock and return { FalseBot, BotFalse } as soon as a state containing False is reached, and it will unblock and return { TrueBot, BotTrue } as soon as a state containing True is reached. The trouble with such a threshold read is that there exist states, such as FalseTrue and TrueFalse, that could unblock either activation set. If the left input writes False and the right input writes True, and these writes occur in arbitrary order, then the threshold read will return a nondeterministic result, depending on the order in which the two writes arrive. With the incompatible threshold set we showed, the threshold read would deterministically return False – although, if the True arrived first, the read would have to block until the False arrived, whereas if the False arrived first, it could unblock immediately.
How is this different? How is it better?
In the formulation of threshold reads I’ve just described, a threshold set is a set of sets of states. In the old way of doing things, though, a threshold set was merely a set of states.
For instance, under the old system, if we wanted to do a (non-short-circuiting!) threshold read from our LVar, we could just use the threshold set
{
TrueTrue,FalseTrue,TrueFalse,FalseFalse}
and the threshold read would unblock and return a particular element, such as TrueFalse, whenever that element was reached or surpassed.
Incompatibility played an important role in the old formulation of threshold sets, too: all the elements in a threshold set had to be pairwise incompatible. In the new formulation, the elements of each activation set have to be incompatible with elements of every other activation set, but the activation sets themselves don’t have to be pairwise incompatible. Indeed, in our example, FalseBot and FalseTrue are quite compatible with each other, even though they’re in the same activation set. The important thing is that they, and all the other elements of that activation set, are incompatible with TrueTrue.
Since elements of each activation set have to be incompatible with elements of every other activation set, we have a way to mechanically turn old-style threshold sets into new-style threshold sets and retain the old semantics: just have every member of the old-style threshold set become a singleton activation set. So, instead of the old-style threshold set
{
TrueTrue,FalseTrue,TrueFalse,FalseFalse}
we’d have
{ {
TrueTrue} , {FalseTrue} , {TrueFalse} , {FalseFalse} }
which is perfectly legal under the new formulation. It retains the non-short-circuiting semantics of the old formulation, though. To fix that, we can combine the latter three activation sets into one activation set, and throw in FalseBot and BotFalse to boot, giving us
{ {
TrueTrue}, {FalseBot,BotFalse,FalseTrue,TrueFalse,FalseFalse} }
which is in fact exactly the new-style threshold set proposed above.
In retrospect, I think that the F state in the so-called “lattice” of the original, flawed formulation was reaching for something like activation sets. It tried to collapse different states containing False into one state, just like the activation set of all the states containing False does. The difference is that, with the new formulation, this collapse happens just a bit later, at reading time, rather than at writing time.
I don’t know if there is a way to mechanically translate from old-style threshold sets to those that allow short-circuiting. I also don’t know how to find out if a given program is “as short-circuiting as it can be”. (I think the idea of “short-circuiting” generalizes beyond this parallel-and example, and that there is in general a tension between determinism and short-circuiting.) I also don’t know if there is a lattice-theoretical or category-theoretical interpretation of what is going on with our activation sets. If you know of one and can explain it to me, I’d really appreciate that!
Where to read more
My collaborators and I have been mulling over this new formulation of threshold sets for a while, and we mentioned it in passing in a recent paper. The first place that it’s been spelled out in detail, though, is in a new draft paper that we just submitted.
The new paper is mostly about what it means to do LVar-style threshold queries of distributed data structures, which I haven’t discussed at all here, but we decided to describe this new, more general form of threshold read while we were at it. Parts of this post are from section 2 of that paper, so if you’ve read this far, you already have a head start on the paper.
Comments welcome!

Comments