Verified causal broadcast with Liquid Haskell

Last week at IFL in Copenhagen, I gave a talk on my research group’s work on using Liquid Haskell to verify an implementation of causal broadcast! This post is a pseudo-transcript of my talk, with some slides included. I’ve also posted the full set of slides if you’d like to peruse those.¹

Update (October 25, 2022): Since IFL, I’ve given a longer version of this talk a couple times. Here are the slides for the longer version, which has more details about our causal delivery proof and a little more information about the architecture of applications that could be built using our library. For even more details, take a look at our draft paper or our GitHub repo.

Hi!

I’m Lindsey Kuper, and I’m an assistant professor at the University of California, Santa Cruz, where I’m part of the LSD Lab (that’s the Languages, Systems, and Data Lab, in case you were wondering). I’m very excited to be traveling internationally again, after three years of not doing that!

This is work that was led by my PhD student, Patrick Redmond, with help from another one of my PhD students, Gan Shen, and our collaborator, Niki Vazou at IMDEA.

Lately I’ve been interested in using language-integrated verification tools to help us build distributed systems that are guaranteed to work like they’re supposed to. The particular guarantee that we’re concerned with here is something called causal delivery of broadcast messages, which I’ll explain with examples in the first part of the talk. The language-integrated verification tool that we’re using is the refinement type system and the accompanying theorem-proving features that are built into Liquid Haskell, and I’ll talk about that in the second part of the talk. So, let’s jump in!

The problem

So as I mentioned, this is my first international travel in about three years. Not too long before the trip, I realized that I didn’t know where my passport was, so I sent a message to my coauthors in our group chat, saying “Oh, no! I lost my passport.” These are messages being sent over an asynchronous network, the Internet, so there’s no bound on how long they might take to arrive at their destination and some might take longer than others. The message to Patrick took a little longer than the rest of them did. That’s to be expected in such systems. Let’s also suppose for now that the underlying message transport mechanism doesn’t inherently give you any guarantees about message ordering.

Found what?

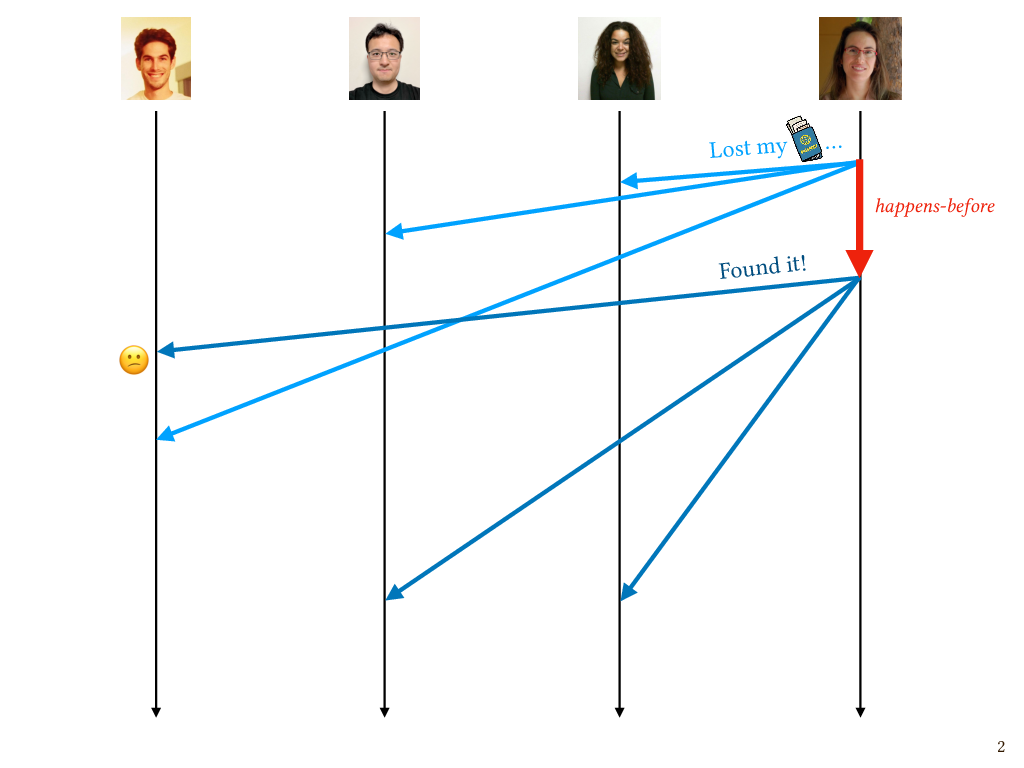
Fortunately, a little later I found my passport (this is a true story, by the way) and let everyone know. Unfortunately, this second message overtakes the first message on the way to Patrick, and so Patrick was confused because he saw this “Found it!” message and didn’t have the context.

This is one example of a violation of what’s known as causal message delivery. The send of my lost passport message happens before the send of my “Found it!” message, in the sense of Lamport’s happens-before relation. Since the sends are ordered in this way, so should the corresponding deliveries on the recipient’s end. In particular, this is a special case of a causal message delivery violation known as a FIFO delivery violation: the messages are both from the same sender and they both go to the same recipient, so they should arrive as though they are coming through a FIFO queue, and if that isn’t what happens, it’s a violation of FIFO delivery.

FIFO delivery helps.

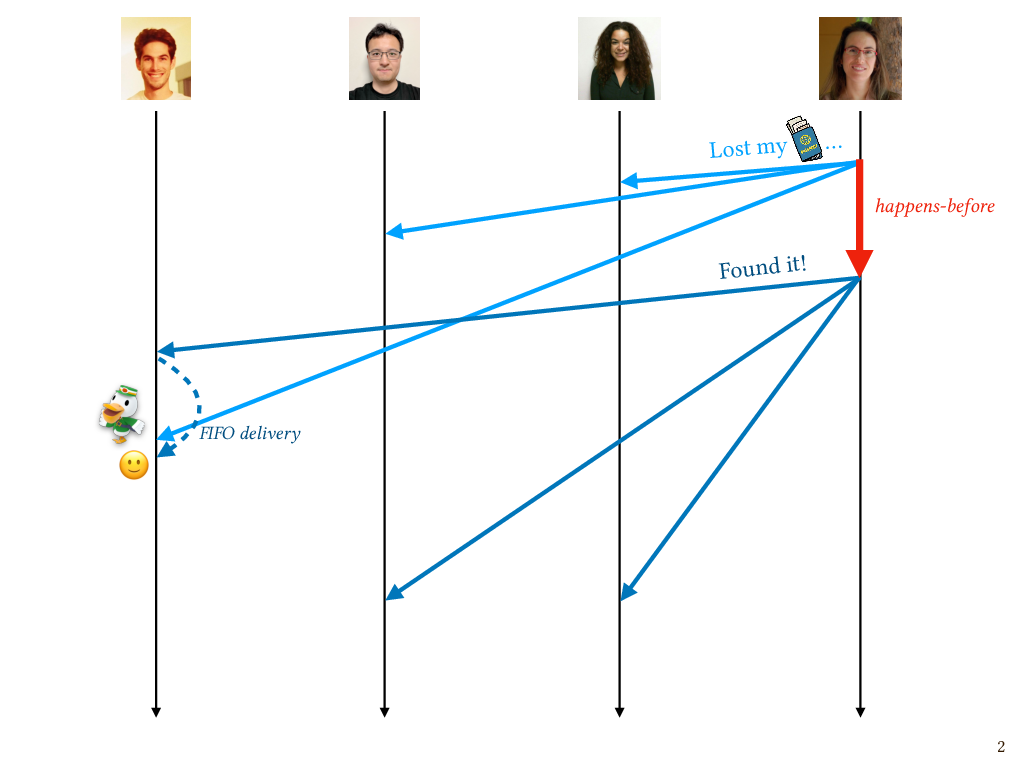
One way to address this problem is to decouple message reception from message delivery. Receiving a message is something that happens to you; you don’t control when it happens. Delivering a message, on the other hand, is something the recipient can control. Imagine a little mail clerk hanging out on Patrick’s process. The mail clerk intercepts each incoming message and chooses to either sit on it in the mail room for a while, or hand it off right away to the application that might be waiting for it, such as Patrick’s chat client. In this case the mail clerk can choose to delay the message until after the previous one from me has been received and delivered, and only then deliver it.

Now, it turns out that FIFO violations are relatively easy to deal with. In fact, if we happen to be communicating over TCP and the messages in question are sent within the same TCP session, then FIFO violations are already ruled out by TCP’s built-in message ordering guarantees, and so the mail clerk wouldn’t need to do anything.

FIFO delivery doesn't solve all our problems.

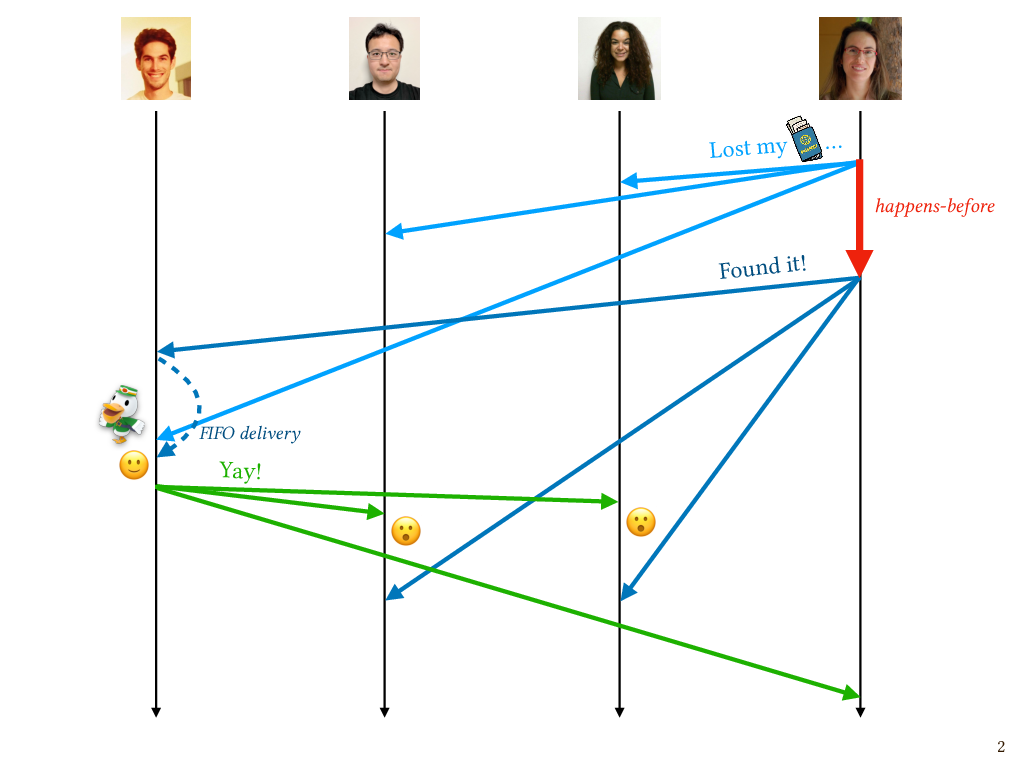
But all is not well! Patrick was happy to hear that I found my passport, so he sent a nice message back. This is yet another asynchronous message. Unfortunately, Gan and Niki now both saw the “Yay!” message after seeing the “lost passport” message from me, but before seeing the “Found it!” message from me. So from their point of view, Patrick was celebrating the fact that my passport is lost. Maybe they thought Patrick was being rude or sarcastic, which wouldn’t be like him at all.

This is another violation of causal delivery. In this case, the send of my “Found it!” message happens before the send of Patrick’s “Yay!” message, which we can see by following these messages forward through time and seeing that Patrick’s send is reachable from my send. So these messages can be said to have an order according to happens-before; they’re not concurrent messages. But for Gan and Niki, the messages were delivered in an order that was inconsistent with that happens-before order. And this time, because the messages came from different senders, the FIFO delivery that we already get from protocols like TCP will do nothing to help us. So we need the mail clerks on these processes to do something to ensure that messages are delivered at their intended recipient in an order that respects the happens-before order.

We need causal delivery.

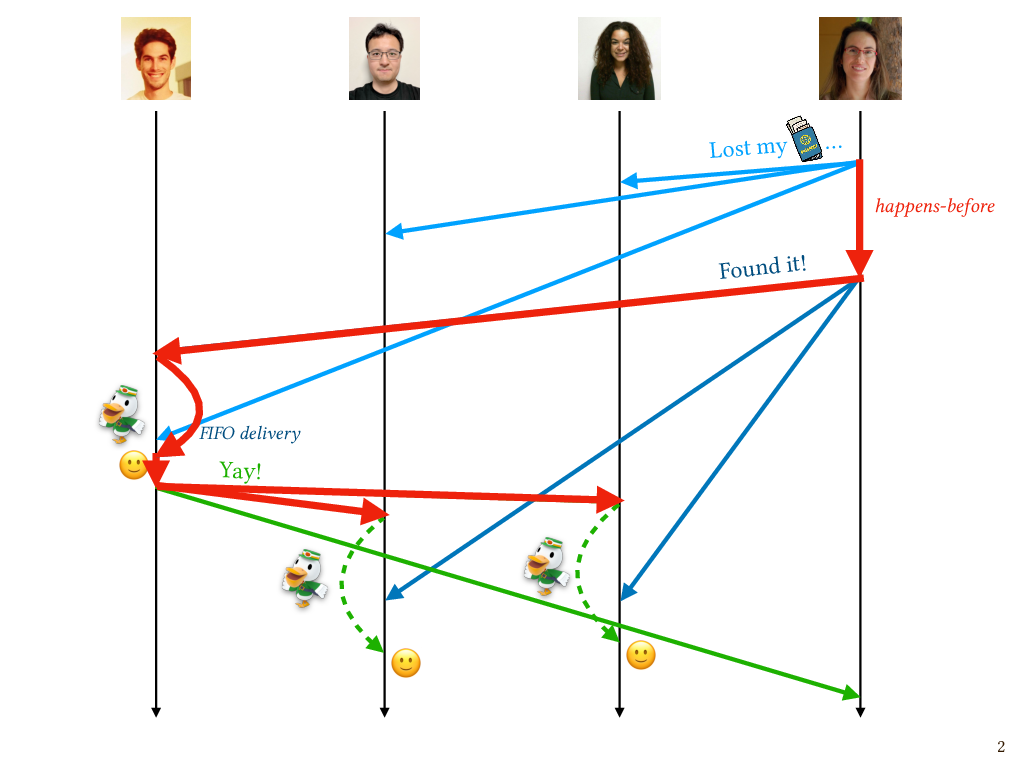
Mechanisms that do this have been well known and widely used in the distributed systems literature for decades. A typical approach is to attach a piece of metadata to each message that summarizes the causal dependencies of the message in a way that can be efficiently checked on the receiver’s end. Our notional “mail clerk” can use this metadata to determine the causal relationship between messages, if there is one, and delay the delivery of a message to a process until every causally preceding message has been delivered. There’s a classic algorithm for this, developed by Ken Birman and collaborators in the 90s. Let’s take a look at how it works.

Causal broadcast with vector clocks

Birman et al.'s causal broadcast protocol.

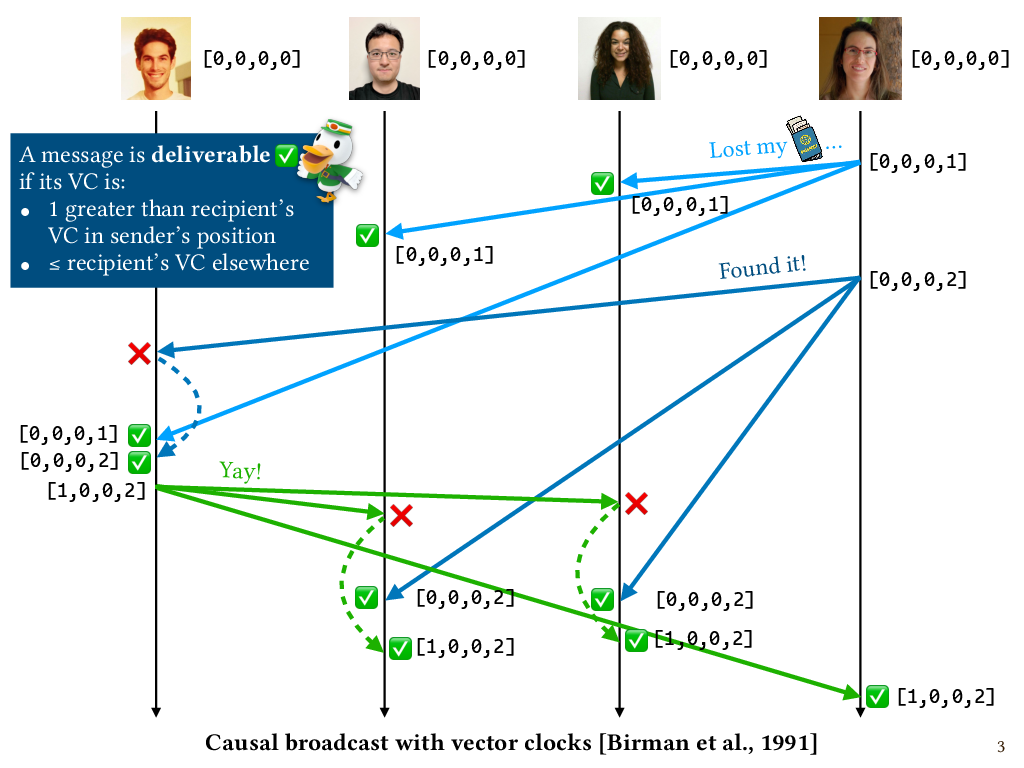
In the Birman et al. causal broadcast algorithm, each process keeps track of a vector with the same number of entries as there are processes, initialized to all zeroes. Intuitively, this vector tracks the number of messages that the process has delivered from each of the processes, including itself. Initially, nobody has delivered any messages, so everyone has a vector of zeroes. This data structure is known as a vector clock, or VC for short. Whenever a process broadcasts a message, it first increments its own entry in its vector clock by one. So for example, when I send my “Lost my passport” message, the last entry in my vector changes from 0 to 1. I then attach that vector clock to the outgoing message as metadata.

Whenever a process receives a message, the mail clerk checks if it’s deliverable. Here’s the deliverability policy our mail clerk uses: a message is deliverable if the attached vector clock is 1 greater than the recipient’s vector clock in the sender’s position, and less than or equal to the recipient’s vector clock in every other position. So let’s look at how that plays out in this execution.

When my first message gets to Niki with the [0,0,0,1] vector clock attached, it is indeed one greater than Niki’s VC in my position and equal to Niki’s VC everywhere else. So it’s deliverable. Niki delivers the message and updates her process VC to the maximum of her own VC and the message VC. Same thing happens for Gan.

Now, here comes the “Found it!” message from me. When I send the “Found it!” message, I again increment my own position in my VC before attaching it to the message, so the message VC is [0,0,0,2]. When the message gets to Patrick, it’s not deliverable, since its VC is one too big in the sender’s position. So the mail clerk holds on to it. Then my first message shows up for Patrick. That one is deliverable according to the mail clerk’s policy. So it’s delivered, and Patrick’s process VC gets updated to the maximum of his own VC and the message VC.

Now the undeliverable message has become deliverable, so that one gets delivered too, and Patrick’s process VC gets updated to the maximum of the two again.

Next, Patrick sends his own message. To do so, he increments his own entry in his VC. So his VC is now [1,0,0,2]. Intuitively, the 1 represents his own message and the 2 represents the two messages from me that causally precede it. Patrick’s message shows up at all the recipients. I can deliver it right away and update my VC to the maximum of its VC and my VC. But for Gan and Niki it has to be queued, because their process VCs are still at only 1 in the entry representing me. They have to wait for the “Found it!” message to show up from me.

When that message shows up, it’s deliverable for both of them, so they deliver it, and then they can deliver the “Yay!” message that was delayed. And now we’re finally done, with everyone’s vector clocks in agreement and all the messages having been delivered in causal order.

That’s the protocol in a nutshell. Protocols like this are ubiquitous in distributed systems, and their implementation is often quite fiddly and error-prone, so that motivates the need for mechanically verified implementations.² In particular, what we want to do is guarantee with a machine-checked proof that if you run this protocol, where each of these processes is locally doing this low-level twiddling of vector clocks, then globally, across the entire execution, all messages will be delivered in causal order. That’s precisely what we did, using Liquid Haskell.

So I’m now going to switch gears to talk a little about what Liquid Haskell is and how it works, and then we’ll come back to how we can use Liquid Haskell to express this causal delivery property of executions.

Refinement types

We can use refinement types to tighten up the type of the vector clock merge operation.

Liquid Haskell adds refinement types to Haskell. For the purposes of this talk, I’ll define refinement types as data types that let programmers specify logical predicates that restrict, or refine, the set of values that can inhabit the type. I’ll give some simple examples, using Liquid Haskell syntax.

For instance, we can define a Nat type that refines Haskell’s built-in Int type with a refinement predicate that says that our Int has to be no less than zero. This is kind of the Hello World of refinement types, but it turns out to be pretty handy to us, because we can represent our vector clocks as lists of Nats.

type Nat = { v:Int | v >= 0 }

type VectorClock = [Nat]

What operations should this VectorClock type support? We need to do things like compare vector clocks, merge them, and so on. Let’s consider the merge operation. When a process delivers a message, it needs to combine its own vector clock with that of the received message by taking the maximum of corresponding vector clock entries. The implementation of merge is straightforward; we use Haskell’s zipWith and take the maximum of corresponding vector clock entries.³

vcMerge :: VectorClock -> VectorClock -> VectorClock
vcMerge = zipWith max

Now, let’s use refinement types to tighten up the type of vcMerge some more. For example, we want the vector clocks we’re merging to have the same length. Let’s start by implementing a type of vector clocks of a given length:

type VCsized N = { vc:VectorClock | len vc == N }

VCsized is the type of a vector clock indexed by a length N. Now we can define a type for a vector clock that’s the same length as another specified vector. I’ll call that VCsameLength.

type VCsameLength V = VCsized {len V}

(By the way, these curly braces around len V in the type are Liquid Haskell syntax to show that that’s an expression argument to a type.)

With our VCsameLength type defined, we can write a signature for vcMerge that expresses the precondition that the vector clocks we’re merging are of the same length, and the postcondition that the returned VC will have the same length as the argument VCs did. And the implementation of vcMerge is still the same.

vcMerge :: v:VectorClock -> VCsameLength {v} -> VCsameLength {v}
vcMerge = zipWith max

Let’s use this version of vcMerge instead.

Refinement reflection

We can use refinement reflection to prove that the vector clock merge operation is commutative.

So far, this is all pretty much what you would expect from a refinement type system. Where I think Liquid Haskell really shines, however, is where it lets you go beyond specifying preconditions and postconditions of individual functions, and lets you extrinsically verify properties that are not captured by a single function’s type, using a mechanism called refinement reflection.

Let’s use refinement reflection to prove that our vcMerge function in commutative – that is, that the order of the VC arguments we give it doesn’t matter.

I’ll do this by defining a type Commutative. This is the type of a Haskell function that returns a proof that a given binary function, A, is commutative. In fact, it returns a value of this Proof type, which in Liquid Haskell is just a type alias for Haskell’s () (unit) type. The value of Proof type is refined by a predicate that expresess the commutativity of that function A.

type Commutative a A = x:a -> y:a -> { _:Proof | A x y == A y x }

With the definition of Commutative in place, we can now state the property we want to prove. vcMergeComm says that given any size N, vcMerge is commutative when applied to two vector clocks of length N. In fact, vcMergeComm is the type of a function that returns a proof of this when given a size N and any two vector clocks of that size.

vcMergeComm :: n:Nat -> Commutative (VCsized n) vcMerge

Now we can prove commutativity of vcMerge by filling in an implementation of vcMergeComm to inhabit the type we wrote down. Here it is:

vcMergeComm _n []      []      = ()
vcMergeComm n  (_x:xs) (_y:ys) = vcMergeComm (n - 1) xs ys

The proof is by induction on the structure of vector clocks. The base case, in which both VCs are empty lists, is automatic for the SMT solver, so the body of the base case need not say anything but (). The inductive case is not automatic, but it is a one-liner; it has a recursive call to vcMergeComm.

In general, Liquid Haskell programmers can extrinsically specify arbitrary properties in refinement types, and the programmer can then prove those properties by writing programs that inhabit those refinement types. Liquid Haskell provides a library of proof combinators that you can use to chain together bits of evidence and build up a proof.

So, Liquid Haskell can do more than traditional refinement types. It doesn’t just let you give more precise types to programs you were writing anyway; it also lets you use refinement type annotations as a place to specify any property about your code that you might want to prove. You can then assist the SMT solver in proving that property by writing Haskell programs to inhabit those types.

Being based on Haskell also lets programmers gradually port code from plain Haskell to Liquid Haskell, adding richer specifications to code as they go. For instance, a programmer might begin with an implementation of vcMerge with the original type we had, VectorClock -> VectorClock -> VectorClock, later refine it to the fancier refinement type we have here, yet later extrinsically prove the property vcMergeComm, and still later use the proof returned by vcMergeComm as a premise to carry out another, more interesting extrinsic proof. And that’s the sort of workflow that we often use.

Causal delivery as a refinement type

Causal delivery as a refinement type.

Let’s return to causal broadcast. The protocol I described earlier was introduced by Ken Birman et al. in the early 90s in the context of their Isis system for fault-tolerant distributed computing. The protocol ensures that when a process receives a message, that message is delayed if necessary and then delivered, meaning applied to that process’s state, only after any causally preceding messages have been delivered. In particular, if the send of message \(m\) happens before the send of message \(m'\), in the sense of Lamport’s happens-before relation, then we know that on all processes, the delivery of \(m\) has to precede the delivery of \(m'\).

As we saw earlier, this is done by using vector clocks to represent causal dependencies, and delaying messages in a queue on the receiver’s side until it’s okay to deliver them. The deliverability check is done by comparing the receiving process’s vector clock with the vector clock of the message.

We used Liquid Haskell to verify that the causal delivery property holds of our implementation. To do this, we first need to express causal delivery as a refinement type.

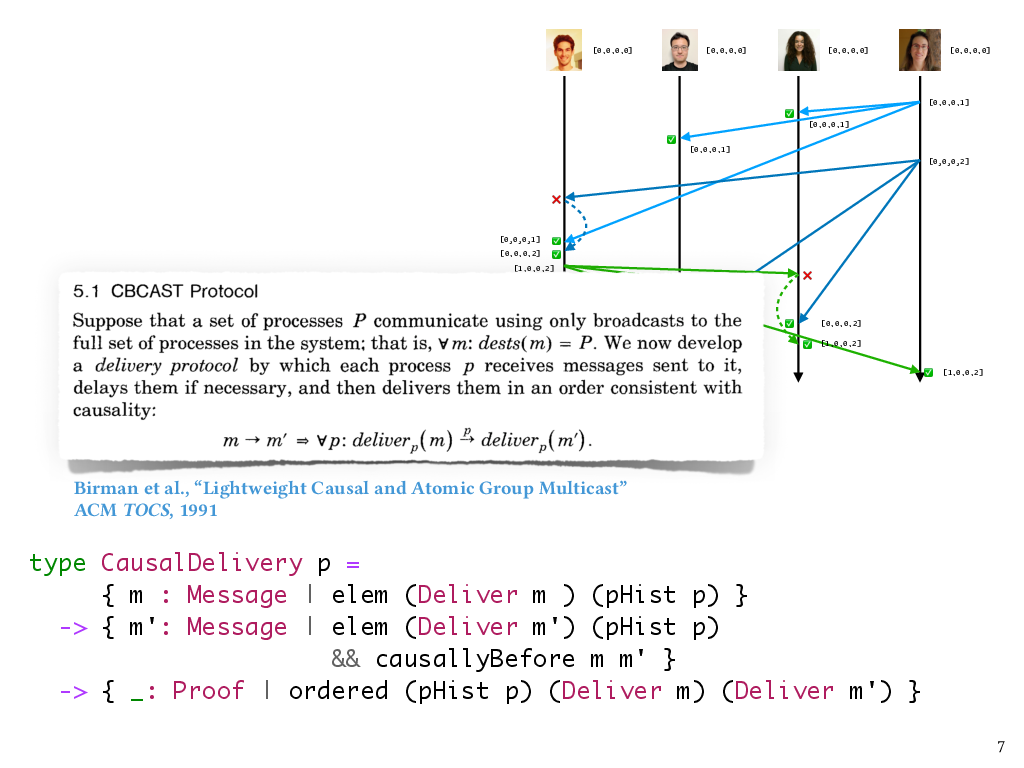
Here’s a simplified look at how we can use refinements in Liquid Haskell to express the type of a process that observes causal delivery. So, a process keeps track of the events that have occurred on it so far, including any messages it’s delivered – and that sequence of events comprises its process history. This type, CausalDelivery, says that if any two messages m and m’ both appear in a process history as having been delivered, and m causally precedes m’, then those deliveries have to appear in the process history in an order that’s consistent with their causal order.

type CausalDelivery p =
     { m : Message | elem (Deliver m ) (pHist p) }
  -> { m': Message | elem (Deliver m') (pHist p)
                     && causallyBefore m m' }
  -> { _: Proof | ordered (pHist p) (Deliver m) (Deliver m') }

So this is essentially taking the definition of causal delivery from the Birman et al. paper and turning it into a property that we can enforce about a process in Liquid Haskell. Now that we’ve defined this type, the verification task is to ensure that for any process history that could actually be produced by a run of the CBCAST protocol, this causal delivery property holds.⁴

Causal delivery preservation as a refinement type

Ensuring that a process observes causal delivery.

The way that we accomplish this is to express the CBCAST protocol in terms of a state transition system, where states represent the states of processes, and state transitions are the operations that broadcast, receive, or deliver messages. Here, the Op type represents those three kinds of state transitions, and the step function takes us from process state to process state.

We can then prove a property that I’ve called causalDeliveryPreservation here, which says that if a process observes causal delivery to begin with, then any process that could result from a sequence of state transitions produced by the protocol will observe causal delivery, too.⁵

This property took a few hundred lines of Liquid Haskell code to prove, with the most interesting part, of course, being the part that dealt with deliver operations. The proof development as a whole is about a thousand lines.

A couple things to mention here. One is that we found that the real key was implementing the protocol in terms of a state transition system. This wasn’t the way it was described in the original paper, although of course all the ideas were there. But we found that that’s what we needed to do to be able to express and prove properties like this, and it took a while for us to arrive at that design, even though it seems obvious in retrospect.

Another thing: the property that I’ve written down on this slide is actually just a property of an individual process, but what we really want is a property of entire executions – we want to be able to say that if this property is true of every process individually then the entire execution observes causal delivery as a whole. To do that we had to define a global state machine and a global transition system, and I’m happy to report that a little earlier this month we, and by “we” I mean my student Patrick, were able to get that global proof done. A cool thing about it in my opinion is that since we’re leveraging the correspondence between vector clocks and happens-before and taking it as axiomatic, we really don’t need anything fancy to make this connection from local to global work.

I’ve always thought vector clocks were really neat, because they let you take something as ineffable and mysterious as causality, and boil it down to something as simple and concrete as a vector of natural numbers. But now after doing this project, I think they’re even cooler, because they let you take something like a happens-before relationship that’s spread out over a whole execution, and boil it down to a property that’s locally checkable. So you get a sort of “local reasoning for free”, which I love!

A plea for help

The blue-sky vision.

All that said, I now want to make a plea for help!

The blue-sky vision of this work is that we want programmers to be able to mechanically specify and verify interesting correctness properties, not just of models, but of real, executable implementations of distributed systems. Moreover, they should be able to do this using verification capabilities integrated into the same general-purpose, industrial-strength programming language that they use for implementation.

Many of us are already sold on language-integrated verification by means of expressive type systems, and I think that our results so far suggest that with Liquid Haskell, it is possible. Unfortunately, I think it’s still way too hard to do.

Thanks to refinement reflection, Liquid Haskell can be used to turn Haskell into a proof assistant, and make no mistake, I think it’s great that this is possible at all. But developing long proofs in Liquid Haskell is still quite painful. It provides only very coarse-grained feedback – either it reports a type error or it doesn’t. We’ve been thinking about how to improve the situation, and one of our proposals is to extend Liquid Haskell with support for Agda-style typed holes, and interactive editing commands that take advantage of them. We published a short paper about this idea at the HATRA workshop last year, but it’s still no more than an idea, and there’s a lot of work to do, so I would invite collaboration from anyone who’s interested in helping out here.

Tak!

Thanks!

To conclude, we saw that we can use Liquid Haskell’s refinement types to express and prove properties about the order in which messages are delivered in a distributed system, which should enable easier implementation and verification of applications on top of the messaging layer. Our code is on GitHub, so give it a try! Finally, while Liquid Haskell is up to the task for projects like this, we still think it could be much easier to use, and we look forward to continuing to improve it.

Thank you for listening!

1. This talk has some overlap with my FLOPS talk back in May, but it’s less broad and more deep; it focuses on this causal broadcast project in particular. If you want a higher-level overview, check out the FLOPS talk instead. ↩

2. If you want to see a protocol that’s kind of like this one but even more fiddly, check out the Raynal et al. causal unicast protocol. ↩

3. This is a simplification: in our actual code, instead of literally writing zipWith max, we had to use our own reimplementations of zipWith and max that have essentially the same semantics as the Haskell Prelude versions, but which are reflected so that we can use them in the definition of a function that gets called inside a refinement predicate. ↩

4. In our actual proof development, the property I’m discussing on this slide is called PLCD, which stands for “process-local causal delivery”. Process-local causal delivery is a property that’s true or not true of a process, while causal delivery is a property that’s true or not true of an entire execution that spans multiple processes. We also define causal delivery in our proof development and ensure that executions of the protocol observe causal delivery, but I didn’t talk about that at length here. Also, the real PLCD is expressed in terms of vector clock comparisons, while on the slide I merely wrote causallyBefore without explaining how that was implemented. In our proof development we rely on two axioms that say that vector clocks preserve and reflect the happens-before relation; this is a classic result, but we don’t have a mechanized proof of it in Liquid Haskell (at least, not yet). ↩

5. In our actual proof development, this property is called trcPLCDpres and is phrased slightly differently. ↩