Conflict resolution in collaborative text editing with operational transformation (Part 2 of 2)

by Abhishek Singh ⋅ edited by Devashish Purandare and Lindsey Kuper

Introduction

In this post we continue the discussion on collaborative text editing started in my previous post. The goal of part 1 of the post was to provide an overview of the dOPT operational transformation algorithm from Ellis and Gibbs’ “Concurrency control in groupware systems” paper and how it addresses the problem of conflict resolution in collaborative text editing. We looked at the problem through a toy example under a set of assumptions that limited the scope of the problem. In this post we remove some of those assumptions and discuss the details of the dOPT algorithm as discussed in the paper.

Here’s the list of the assumptions I made in my previous post:

1. Operation messages from either site are received exactly once.
2. There are exactly two editors in the system: one at Alice’s end and the other at Bob’s end.
3. My implementation does not use clocks to timestamp operations, so the happens before relationship is established based on message delivery. It is assumed that LOCAL and REMOTE operations happen concurrently.
4. Operations are processed in the order in which they are seen and executed at each particular site. In our implementation, the executed operations are stored in a list OTEditor.Ops.
5. Unlike the implementation in the paper, we do not assign priorities to an operation. Every operation has equal priority.
6. An operation is sent to others immediately after it was executed at one particular site. There is no out-of-order delivery of messages.

For reference, here’s the example collaborative editing session between Alice and Bob that we looked at last time:

Figure 1. Operations received by Alice and Bob are transformed before being applied to local data.

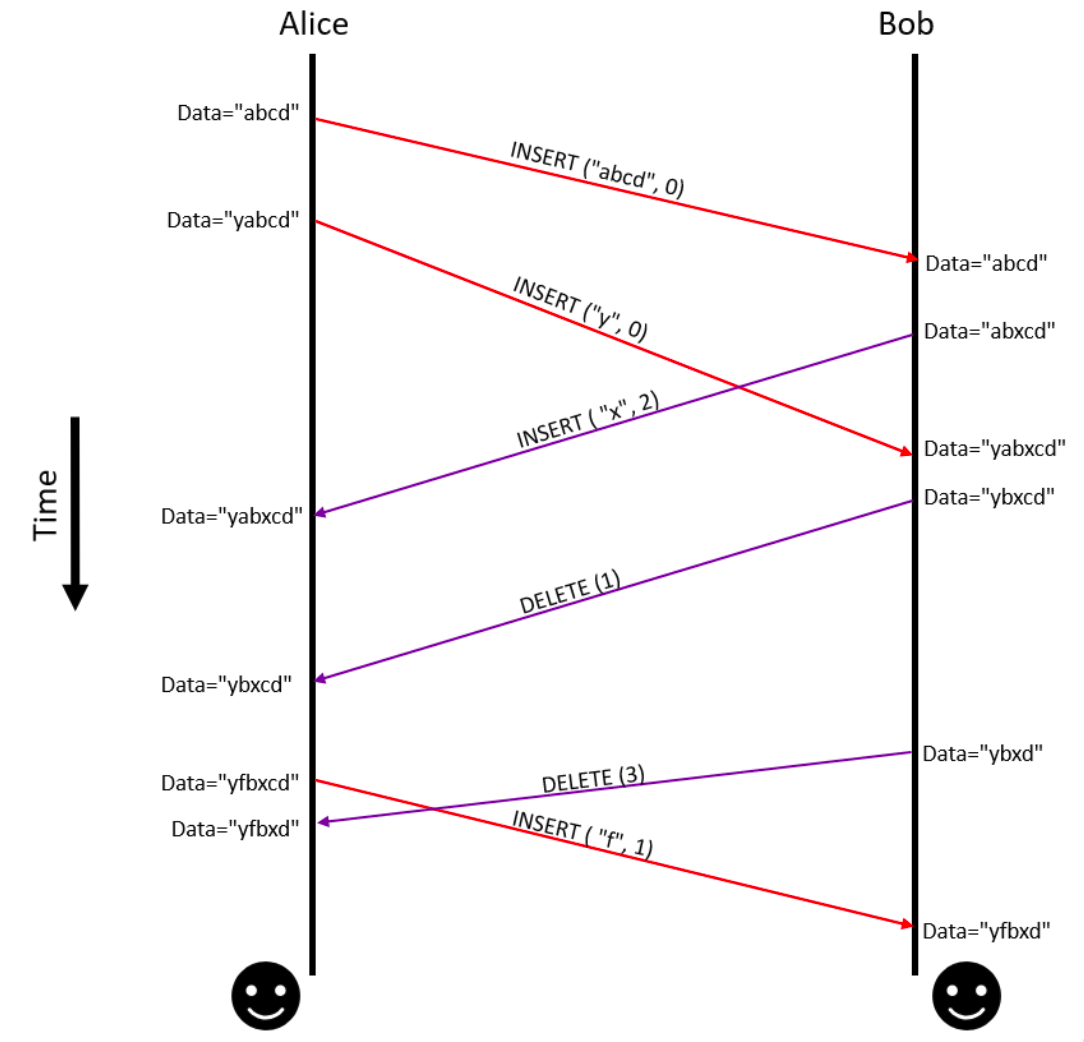
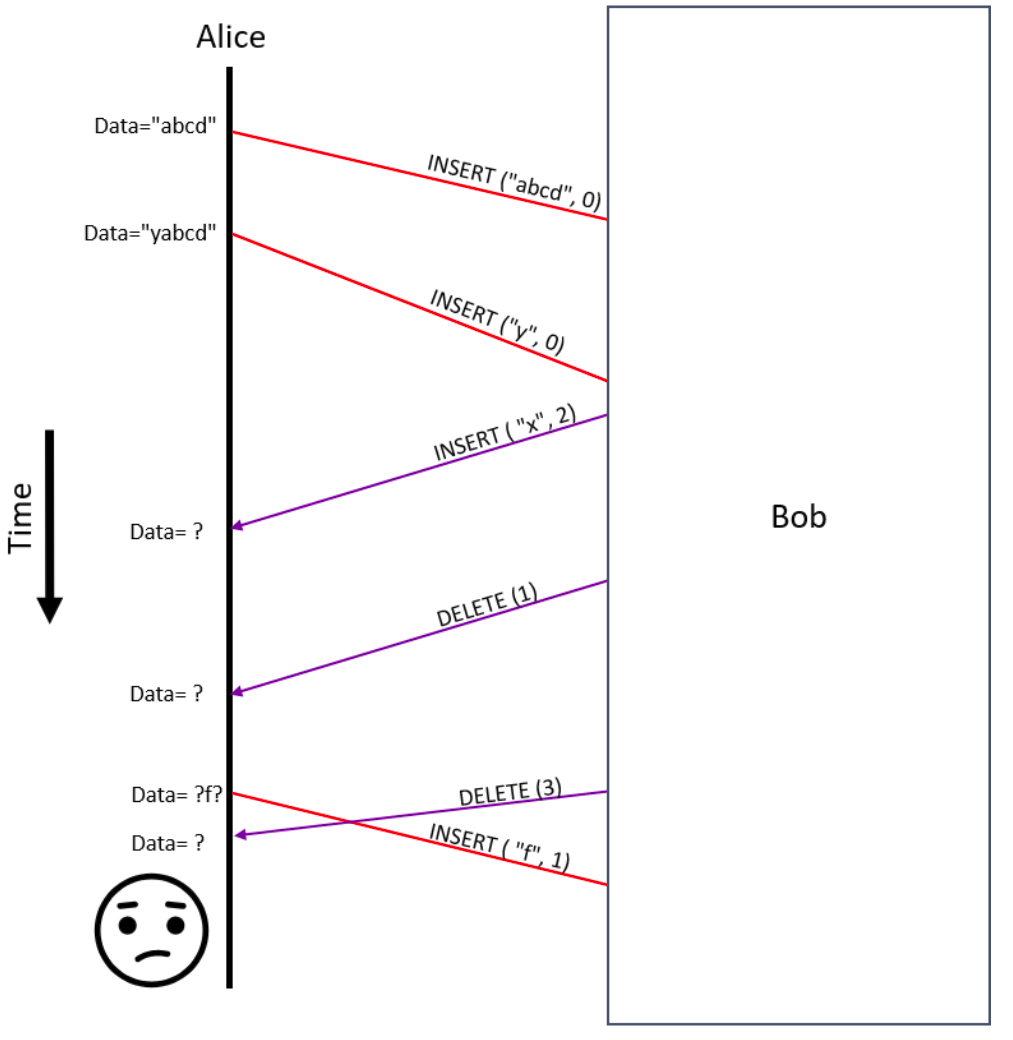
Let us consider the consequences of removing each of the above assumptions. Primarily, there is a problem of ascertaining causality of messages in the design. Consider the second and third operations exchanged between Alice and Bob in Figure 1. There is no way for Alice to know if the operation INSERT ("x", 2) sent by Bob happened before or after Bob received the INSERT("y", 0) operation from Alice (even though we can see the figure and know that the operations were concurrent). Figure 2 shows Alice’s view of the world: Alice cannot know if there is a causal relationship between the operations, because we did not address causality in part 1. The ordering of the messages was enforced only by the order in which the messages were delivered to each user.

Figure 2. Alice does not know how Bob executed the operations at his end and therefore cannot know how received operations should be applied at her end.

The possibility of receiving out-of-order messages is another issue that the design must address. The algorithm in part 1 executes messages on each replica in the order in which they are received. This aggravates the problem of data inconsistency among the replicas if messages were delayed in transit and were not received in the same order in which they were generated. Suppose the operation INSERT ("x", 2) from Bob in Figure 1 was delayed and received by Alice after the DELETE (3) operation from Bob. This would lead to the operations being executed in different orders on Alice’s and Bob’s ends leading to data inconsistency between the replicas. Since in-order message delivery is subsumbed by causal delivery, we can also solve this problem by addressing causality.

Finally, another assumption we made has to do with the number of users participating in the system. It is relatively easy to understand how operation messages are exchanged when only two users exist in the system. With more users, the number of messages needed to share changes with other users grows. If there are n users in the system, every state change at one user must be communicated with n-1 users. With each user making changes to their document replica, the version of dOPT developed for the two-user collaborative text editor developed in part 1 cannot be used, as there is no way of knowing the exact state of a replica when an operation was executed.

Precedence, convergence, and quiescence

The crux of the data consistency problem discussed until now is that a site does not know the historical trace of an operation when it receives the operation request. The approach proposed for dOPT in Ellis and Gibbs’s paper involves the use of a vector clock to order the operations generated on different sites (each site or user is associated with a single document replica). The paper defines a Convergence Property and a Precedence Property and a notion of quiescence to describe the correctness of the algorithm. The authors define the properties as follows:

The Precedence Property states that if one operation, o, precedes another, p, then at each site the execution of o happens before the execution of p.

A groupware session is quiescent iff all generated operations have been executed at all sites, that is, there are no requests in transit or waiting to be executed by a site process.

The Convergence Property states that site objects are identical at all sites at quiescence.

The Precedence Property makes use of the precedes relation, which is reminiscent of Lamport’s “happens-before” relation. If an operation o precedes p, then the Precedence Property ensures that o is executed before p everywhere.

The Convergence Property combined with the notion of quiescence is nearly identical to the Strong Convergence property defined by Shapiro et al.. In the Ellis and Gibbs paper, however, quiescence is enforced periodically. The detection of quiescence is done via a distributed consensus algorithm, which is not discussed in the paper.

The Distributed Operational Transformation (dOPT) algorithm

The dOPT algorithm in essence is an attempt to order operations for execution by maintaining their causal links to other operations and, based on that order, decide whether transformation of the operation indices are really needed when executed by individual sites. The dOPT algorithm described in the paper assumes a constant number of sites. For every change that a site makes to its replica, a request is generated and sent to other sites. To achieve the two properties the design uses a request queue Q_i and a request log L_i, where the subscript i is the site identifier. Throughout the rest of the discussion, site i will be the location where the request is being processed and site j will be the site which sent the request.

The request queue contains operation requests either sent by remote sites (j) or from the user of the current site (i). These are requests that are waiting to be processed, and the queue acts as a buffer where all incoming requests are stored for further processing. The request log, on the other hand, is a log of requests that have been executed by the site. The log is a list of requests ordered by the order in which the requests were executed.

Each request has the form <i, s, o, p>, where i represents the site identifier and s represents the state vector of the site i. The state vector, as discussed by Ellis and Gibbs, is essentially a vector clock that specify when an operation was executed on site j and its relation to the operations in the request queue in site i. o represents the operation to be performed (insert or delete). Finally, p specifies the priority of the operation. As discussed in my previous post, operations must commute with each other.

The dOPT algorithm builds a transformation matrix for the operations that are supported: insert and delete. A 2x2 transformation matrix is created which reflects the cases seen during operation execution: insert-insert, insert-delete, delete-insert and delete-delete. The priority of an operation is used to compute if an operation should be transformed and what the values of the recomputed indexes should be.

The algorithm uses state vectors to order events causally. Given two state vectors s_i and s_j, Ellis and Gibbs define the following relations:

1. s_i = s_j if each component of s_i is equal to the corresponding component of s_j.
2. s_i < s_j if each component of s_i is less than or equal to the corresponding component of s_j and at least one component of s_i is less than the corresponding component in s_j.
3. s_i > s_j if at least one component of s_i is greater than the corresponding component in s_j.

For example, if s_i = [ 1 2 3 3 ] and s_j = [ 1 2 3 4 ], we have s_i < s_j. However, if s_i = [ 4 3 2 1 ] and s_j = [ 1 2 3 4 ], we have s_i > s_j.

During initialization the following operations are done:

1. Set Q_i to empty
2. Set L_i to empty
3. Set s_i to [0 0 ... 0]

The algorithm defines three possible execution states:

1. Operation request generation,
2. Operation request reception, and
3. Operation execution.

During operation request generation the site i generates an insert or delete operation. The operation is not executed immediately; the local data is not modified during operation request generation. Once the request is generated, it is appended to the site’s request queue Q_i and broadcast to all other sites.

Generate operation <i ,s_i , o, p>

Q_i := Q_i + <i ,s_i , o, p>

A request generated on a site j is eventually received by site i which then moves to the “operation request reception” state. In this state, the received operations are appended to the site’s request queue.

Receive operation request from remote site j: <j ,s_j , o_j, p_j >

Q_i := Q_i + <j ,s_j , o_j, p_j >

During operation execution, requests from the request queue are processed. The order of execution of requests in the request queue is determined by the total order of events in the request queue as determined by the comparison of the state vectors. Briefly, in this step the operation from the request queue is chosen based on the executed operations in the request log. We locate the operation older than the current state vector at site i. Transformation is performed based on the operation logs in the request log. Comparison of the state vectors follows the conditions stated previously:

1. If s_j > s_j, this means that the site j has executed operations which site i has not seen yet. So this operation will have to stay in the queue till all operations between i and j have been executed.
2. If s_j = s_j, the two state vectors are identical and operation o_j can be executed without transformation.
3. If s_j < s_j, site i has executed operations not seen by site j. The operation can be applied immediately, but requires operations to be transformed because other changes not visible to site j have already been executed by site i.

The principles behind transformations were discussed in my previous post. The main idea is that the transformations must commute. This allows the operations to be executed in any order. The idea of commutative operations is vital to any operational transformation technique. In fact, the idea of commutative (and associative) operations comes up very frequently in discussions of synchronization-free convergence algorithms in distributed systems. A fairly recent example is in a paper by Attiya et al. when discussing convergence of replica state in their formalization of the RGA protocol for collaborative text editing. Another example is in conflict-free replicated data types, where operation commutativity is key to state convergence.

Final thoughts

The idea of operational transformation originally proposed by Ellis and Gibbs has morphed into a compendium of technologies used to build collaborative systems. A prominent example is the Jupiter collaboration system. Instead of a peer-to-peer system as we have been discussing until now, Jupiter used a centralised architecture where a server maintains a single copy and all operation requests are handled via the server. This system became the basis of the Google Wave and Google Docs projects, as mentioned in my previous post.

Over the course of these two blog posts, I have aimed to understand the key ideas behind the early specification of operational transformation and convey them with some clarity. Although collaborative text editing has been a topic of research since at least the 1980s, writing these posts allowed me to study the problem in some detail and has kindled my interest in building systems where multiple agents can work together towards a common goal. Thinking about building useful abstractions for collaborative computing agents is something that will keep me busy for some time.